01 Theory
In 8th grade, I had the idea for a mathematical theory: 01 Theory. The basic idea is that if you analyzed all numbers, from negative to positive infinity, and counted the number of '1's and '0's that appeared in the numbers (ex. 10165 has 2 '1's and 1 '0') that the 1s would not only out number the 0s, but by an infinite amount.
This is due to the simple fact that a number can start with a 1 but not a 0. In any place that a 0 can appear, a 1 could take its place, but this is not correct the other way around, due to the fact that a number can start with a 1. As a result, there will be an infinite number more 1s than 0s.
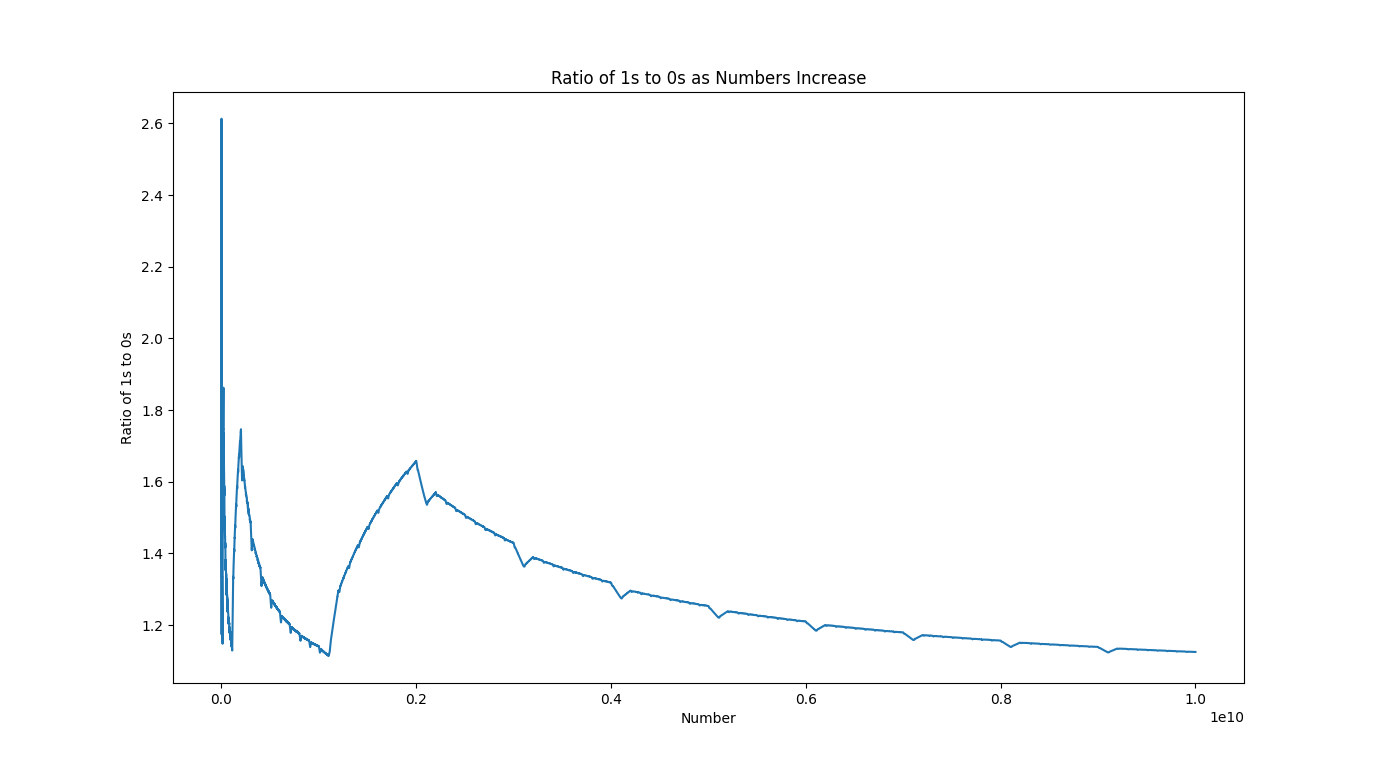
Using my new programming skills, I coded a program in Python that analyzes the ratio between 1s and 0s and uses MatPlotLib to create a graph. The graph can be seen above. As can be seen, the ratio always remains above 1, as there will always be more 1s than 0s, however, the graph tends downward (to an asymptote of 1) as the numbers get larger.
Analysis: This is because if we think about why the ratio is above 1 at all, is because of the first digits of numbers. Without the first digits, the ratio would be exactly 1, as the number of 1s would equal the number of 0s. However, the first digits are accounted for in this calculation, so the ratio is above one. The "value" of a first digit decreases as the numbers get large though, as there are more digits.
For example, the numbers between 10 and 19 all start with a 1, thus adding 10 "1"s to the count of "1"s, and additionally adds 1 "1" for the number 11 and 1 "0" for the number 10. So we're left with 12 "1"s and 1 "0", which is a ratio of 12:1. However, if we look at the numbers between 100 and 199, we see that there are 100 "1"s added due to first digits, but then 10 "1"s and 10 "0"s added because of second digits, and then 10 "1"s and 10 "0"s added because of third digits. This leaves a ratio of 120:20, or 6:1. So we can see that as the numbers get larger, although the number of "1"s will infinitely outpace the number of "0"s, the ratio will approach 1, as the "value" of the first digits decreases as more digits "drown them out".
If you want to take the analysis one step further, you can also see sharp dips along the entire curve. I believe these are caused by sets of numbers beginning with 1 ending. If we look at x=.2 (1e10), we can see a sharp dip that starts exactly at x=.2 (1e10). This is because the from 1 billion to 2 billion (x=.1 1e10 to x=.2 1e10), all the numbers begin wtih a 1, so there is a huge upward spike as we can see. This ratio balances out though, as we hit the 2 billion - 3 billion range, as the numbers not longer start with 1. In addition, I believe the immediate downward spike is because we hit the values 2,000,000 - 2,099,999, which all essentially have a "starting 0" in the second place. This causes a sharp decrease in the ratio, as can be seen with the downard spike. We can then see a bit of a recovery right after though, as we hit 2,100,000 - 2,199,999, sending the ratio back up a bit, as the "1"s recover. It then continues to decay after, as there isn't a significant set of numbers that all have "1"s. If you look closely, you can see mini dips and recoveries on the graph on the "steady decreases" for a smaller version of what I've explained in this paragraph.
This is a super complex and hard to understand theory, so feel free to click any of the social buttions below and contact me. I'd love to explain it more - I could talk about this for hours.